​为什么波函数必定是复函数？看看中科院物理所怎么说的

为什么波函数必定是复函数？看看中科院物理所怎么说的

这个问题的第一感觉是因为，对于波函数，我们观测到的东西是一个实数的概率分布，但是，控制系统演化的波函数却是一个复函数ψ(x,t)。通常的说法（一般教科书）是波函数具有一个不重要的相位因子，也就是U(1)规范自由度。但是真么回答你肯定是不会满意的（我自己也不会满意）~~那怎么理解呢？

让我们以最简单的自旋1/2系统为例，来看看怎么回答这个问题。首先对于自旋态的表示，对于自旋1/2的粒子，它的自旋波函数是一个二分量的波函数

.

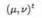
其中μ,ν是两个数，我们先来看看如果波函数必须是一个实的波函数，会怎么样？

.

【实波函数】

那么μ,ν是两个实数，这样的话，再由波函数的归一化条件，我们知道必须满足

.

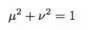
那么我们可以看到，这时候二分量自旋波函数的自由只有一个（因为原先μ,ν两个自由度减去归一化条件一个自由度），那我们知道，自旋本质上是角动量，描述一个方向的角动量，我们知道，至少需要两个自由度（θ，φ）

.

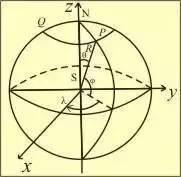
显然，实数的波函数不能够完全描述我们的系统。

【复波函数】

如果μ,ν是两个复数的话，我们知道一个复数有两个自由度，那么现在我们有四个自由度，同样减去归一化的一个约束条件，我们实际上有三个自由度来描写波函数。

.

.

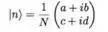
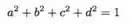
同样的，描述一个角动量的方向，我们同样需要两个自由度（θ，φ），那么剩下一个自由度？是的，这个自由度就是规范自由度，描写波函数整体相位的一个自由度。所以，我们看到，用实波函数来描写量子系统，就会面临描述不完全的情况，而用复波函数来描写量子系统，就会面临自由度增加的情况。那这个增加的规范自由度有什么物理意义么？

由于篇幅的限制，这里就简单的说两句，感兴趣的同学可以自己去维基。对于单粒子的自旋系统，这个多余的相位自由度实际上就是Berry相位，是一个几何相位。最近比较火的拓扑绝缘体就和这个东西有关，同样在超导和超流中，也是由于这个相位选取一个特定值的结果，即所谓的U(1)规范破缺。

总之呢，大自然看似为我们带来了一个未知的自由度的同时，也为我们打开一扇通往新世界的大门~~~~